Assignment 1: Text and Probability
Repository: github.com/wellesleynlp/yourusername-cs349-a1-textprocess
Solution: github.com/wellesleynlp/a1solution
Objective
Become comfortable with text processing and corpus analysis in Python, and the use of probabilities. Explore two canonical problems in NLP: finding collocations and language identification.
Setup
You may not work with a partner for this assignment. Discussion is encouraged, and you may get help on logistical issues (low-level Python features, Git management, etc.) but write all the code on your own.
Install NLTK (a Python library) following the instructions in the "Tools" menu link. NLTK is installed on tempest -- you can work on the assignment there in case you have persistent issues installing it on your own computers.
Clone your starter repository, github.com/wellesleynlp/yourusername-cs349-a1-textprocess. Since some of you may not be fluent in Python, a fair amount of starter code and interface specification is provided. (Future assignments will have progressively less.)
Read and understand the provided code and interfaces thoroughly. Note that the skeleton functions that you need to fill in are marked with "TODO" and contain a placeholder pass body. This is only so you run incomplete code without raising syntax errors. Replace pass with your definitions.
Do not modify any of the provided methods unless asked to do so.
Testing
Test your functions as you write them.
An automated checker with test cases and grade estimates has been pushed to your repositories. It evaluates everything in section a, section b except for the plotting functions, and section c, but not section d.
python verify.pyruns tests on all the sections. To test only a subset of the sections, specify the section names (in any order) as an optional argument.
python verify.py ab
This checker is brand new. Please bear with any teething problems and report issues.
Submitting
Before the deadline (11:59 pm EST on Mon, Feb 08),
push your edited
utils.py,
corpus.py,
ngram.py,
collocations.py,
and identifylang.py
files, as well as the completed README.md and reflection.md,
to your repository following these instructions.
Section (a): Utilities [10 pts]
We'll develop utils.py as a codebase of various functions over the semester.
It currently contains two complete definitions,
normalize and basic_count.
Fill in the functions below following the docstrings and examples in the file.
length_count-
expectation entropy-
tuple_count(a bit more complex than the others)
Section (b): Basic Corpus Statistics [15 pts]
This section is independent of section (a),
but some of the provided code
calls length_count,
expectation,
and entropy
from utils.py.
We have provided various text files of comparable size in data/:
- austen.txt: a collection of Jane Austen's novels from Project Gutenberg
- wikipedia.txt: some articles from English Wikipedia
- kjvbible.txt: King James Version of the Bible from Project Gutenberg
- uniform.txt: a file produced by uniformly sampling from the 26 characters of the alphabet, space,
period followed by space, comma followed by space, and the newline character
Open up
ngram.pyandcorpus.pyand study the code. Write the definitions for these functions and methods incorpus.py:num_hapaxes: Hapax Legomena refer to words in a corpus that occur exactly once. This function takes a dictionary of counts (such as the one returned bybasic_count) and returns the number of items with a count of 1.tokenizereads a file and returns a list of sentences, where each sentence is a list of tokenized words. Lowercase all words if and only if the casefold argument is True. Use NLTK'ssent_tokenize, which splits apart sentences, andword_tokenize, which splits apart words and separates punctuation. The function may take a while (a couple of minutes) to run because of the size of the texts.Corpus.plot_frequses matplotlib.pyplot.loglog to create a plot of word frequency against rank (so we can visualize agreement with Zipf's Law) and saves it to the given filename. Both the x and y axes should be on a log10 scale. For example, the plot forausten.txtis:
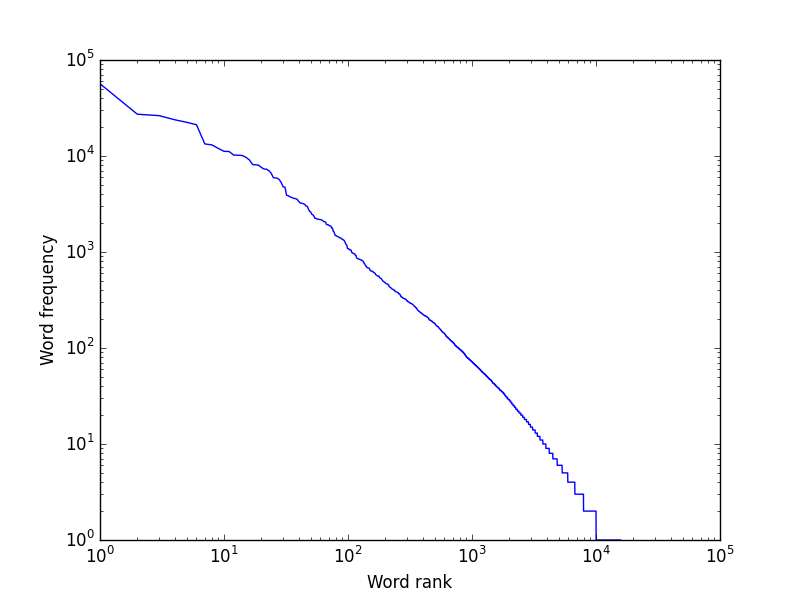
Corpus.plot_lengthsuses matplotlib.pyplot.bar to display bar plots of the number of word tokens and types of each length. The plot forausten.txtis:
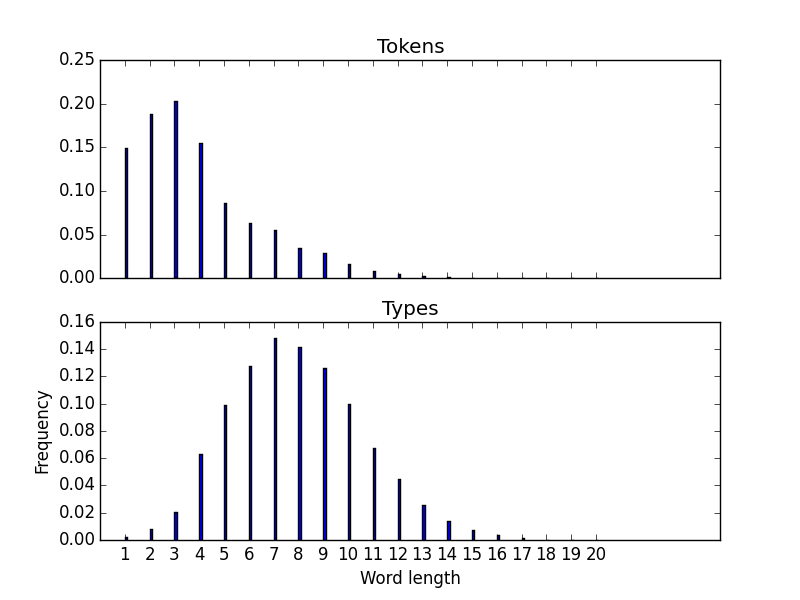
Your plot style (colors, line widths, titles) need not match the examples exactly.- Once you're done, use the program to get a summary of a text's statistics and generated plots.
You can run
corpus.pywith the name of a text file passed as a command line argument, like so:python corpus.py data/austen.txt
Most IDEs allow command line arguments. Canopy lets you specify them after the name of the program in the "run" statement in the console.
This produces the following statistics for
austen.txt, and also generates the plots.32410 sentences
852324 word tokens
15785 word types
54.00 average tokens per type
26.30 average sentence length
3.88 average word token length
7.90 average word type length
Hapax legomena comprise 36.63% of the types
Estimated a 1-gram model over words
',' is the most common word, occurring 6.64% of the time
The unigram entropy is 8.88 bits
Estimated a 1-gram model over characters
'e' is the most common character, occurring 12.05% of the time
The unigram entropy is 4.39 bitsStudy the difference in the numbers produced for the different text files, and briefly write your thoughts in response to the first two questions in
reflection.mdin the repository.Section (c): Language Identification of Scrambled Text [10 pts]
This section is independent of the others.
You've laid your hands on a secret message (
mystery.txtindata/decode), produced by randomly permuting the characters of the original text. While we may not be able to decode it just yet, we can use our information theory chops to figure out which language it was written in.Scrambling means that the unigram distributions of the characters are unchanged from the original message. Operating under the assumption that a character unigram distribution is a reliable signature of a language, use cross-entropy to identify the language of the message:
- Create character unigram models for each language from the provided counts in
{english, spanish, italian, french, german, polish, dutch}.charcounts.
NOTE: TheNGramclass constructor takes three variables:n, which is 1 for this problem,unit(which specifies whether the unit is a "character" or "word") which is "character" in this case, andcountdict, a dictionary of raw counts of each possible character. It creates a dictionary calledself.relcountscontaining the relative frequencies of each unit. - For each model, compute its cross-entropy on the mystery text
(a sequence of characters, with no whitespace or line-breaks).
Implement the
NGram.get_probandNGram.cross_entropymethods inngram.pyto aid with this. - Find the language whose model compresses the mystery text the best
(i.e., has minimum cross entropy on the text).
Write functions named
evaluateandidentifyinidentifylang.py, as indicated by their invocations in the main block. Running
python identifylang.py data/decode
will print the name of the hypothesized mystery language.
Finally, answer the third question in
reflection.md.Later in the semester, we will use probabilistic models to decode certain types of ciphertexts as well.
Section (d): Finding Collocations [10 pts]
This section relies on the correctness of
tuple_countsinutils.pyfrom section (a).Recall that pointwise mutual information between two outcomes, $x$ and $y$, is given by
$\mathrm{pmi}(x, y) = \log\frac{P(x, y)}{P(x)P(y)}$
where $P(x, y)$ is the probability of $x$ and $y$ occurring together. If we define "occurring together" as "words $x$ and $y$ appearing next to each other in sequence", then the $\mathrm{pmi}$ is a measure of how likely it is that the word pair $x y$ is a collocation.
Using some of the methods in
NGramandtuple_countfromutils.py, definepmi_collocationsincollocations.py. This function takes aCorpusobject, an integer k, and an integer threshold, and returns the topkcollocations in the corpus (ordered by the $\mathrm{pmi}$) that occur at leastthresholdnumber of times, along with their $\mathrm{pmi}$ scores in bits.Your collocations should not span multiple sentences (like the last word of one sentence followed by the first word of the next). To avoid this possibility, take care with how you extract the counts for co-occuring words.
Running the program with filename, k, threshold in order will print out the list of collocations in the file along with their scores.
python collocations.py data/kjvbible.txt 5 10
gives
mary magdalene 14.0184371737
committeth adultery 13.6509280445
golden spoon 13.5914270328
tenth deals 13.5590055551
solemn feasts 13.3628026577Answer the fourth question in
reflection.md.Misc [5 pts]
- Answer the last question in
reflection.md. - Fill out
README.mdand submit your work correctly. - Check that your code is reasonably elegant and efficient.
- Create character unigram models for each language from the provided counts in
{english, spanish, italian, french, german, polish, dutch}.charcounts.